逻辑回归(Logistics Regression)

发表于 | 分类于 ， | | 本文总阅读数 次
| 字数统计: 1.4k | 阅读时长 ≈ 6
逻辑回归(Logistics Regression)

lr

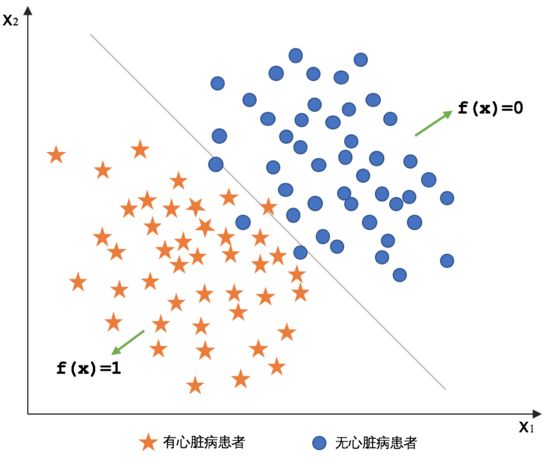
原理解读

  逻辑回归(Logistics Regression):是一种广义线性回归，都具有 w’x+b，其中w和b是待求参数，其区别在于他们的因变量不同，多重线性回归直接将w’x+b作为因变量，即y =w’x+b，而logistic回归则通过函数g将w’x+b对应一个隐状态p，p =g(w’x+b),然后根据p 与1-p的大小决定因变量的值。如果g是logistic函数，就是logistic回归。

核心思想

预测函数

对于二分类问题，$y \in \lbrace 0,1 \rbrace$，1表示正例，0表示负例。逻辑回归是在线性函数$W^Tx$输出预测实际值的基础上，寻找一个假设函数函数$h_W(x)=g(W^Tx)$，将实际值映射到到0，1之间，如果
$$y =\begin{cases} 1 & h_W(x) \ge 0.5 \ 0 & h_W(x) <0.5 \end{cases}$$
逻辑回归中选择对数几率函数(logistic function)
$$g(z)=\frac{1}{1+e^(-z)}$$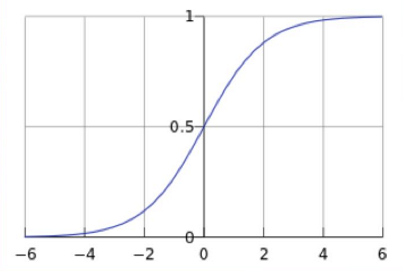
sigmod
有一个非常重要的性质，可以方便我们的计算。
$$g(z)’=g(z) \cdot (1 - g(z))$$

损失函数

我们假设
$$ \begin{cases}P(Y=1|X) = p(x) \ P(Y=0|X) = 1 - p(x) \end{cases} $$
根据极大似然估计可知
$$ \hat{w} = \underset{w}{argmax} \ L(w) = \underset{w}{argmax} \prod_{i = 1}^{N} [p(x_i)]^{y_i} \cdot [1 - p(x_i)]^{1 - y_i} $$
两边同时取对数，计算对数似然函数。
$$ \hat{w} = \underset{w}{argmax} \ ln(L(w)) = \underset{w}{argmax} \sum_{i = 1}^{N} [y_i \cdot ln(p(x_i)) + (1 - y_i) \cdot ln(1 - p(x_i))]$$
因为我们在计算时常常求最小值，因此我们设计损失函数，令$J(w) = -\frac{1}{N} ln(L(w))$
$$ \hat{w} = \underset{w}{argmin} \ J(w)=-\frac{1}{N} \underset{w}{argmax} \ ln(L(w))$$
$$ \hat{w} = -\underset{w}{argmin} \frac{1}{N} \sum_{i = 1}^{N} [y_i \cdot ln(p(x_i)) + (1 - y_i) \cdot ln(1 - p(x_i))]$$
下面转化为求$\underset{w}{argmin} \ J(w)$，使用常见的梯度下降法进行求解。
$$ g_i = \frac{\partial J(w)}{\partial w_i} = (p(x_i) - y_i) \cdot x_i $$
$$ w_i^{k + 1} = w_i^k - \alpha \cdot g_i$$

代码实战

LR_train.m

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
clear;clc;
f_sigmod=@(x)1./(1+exp(-x));
%x为样本，行数代表特征数，列数代表样本数,以列向量的形式输出，label为样本所对应的类别
train_x=[0.5,0.5,0.8,0.2,0.1;...
    0.8,0.7,0.6,0.2,0.4];
%1为第一类，2为第二类
train_y=[1,1,1,0,0];
%特征数
feat_num=size(train_x,1);
%样本数
train_num=size(train_x,2);
%设置最大迭代次数
times=10000;
%学习率
a=0.1;
%权向量
w=rand(1,feat_num+1);
%增广矩阵
x_expend=[train_x;ones(1,train_num)];
for i=1:times
    tem=w;
    %w=w-a/m*Σ(sigmod(wx)-y)x
    w=w-a/train_num*sum(repmat((f_sigmod(w*x_expend)-train_y),feat_num+1,1).*x_expend,2)';
    if sum(abs(w-tem))<5e-3
        break;
    end
end
disp(i)
if i>=times
    disp('The question is not Linearly Separable');
%否则线性可分，写出函数表达式
else
    express=[];
    %输出表达式
    for i=1:feat_num
        if w(i)>0
            express=[express,num2str(w(i)),'x',num2str(i),'+'];
        elseif w(i)<0
            express=[express(1:end-1),num2str(w(i)),'x',num2str(i),'+'];
        end
    end
    if w(feat_num+1)==0
        express=[express(1:end-1),'=0'];
    elseif w(feat_num+1)>0
        express=[express(1:end),num2str(w(feat_num+1)),'=0'];
    else
        express=[express(1:end-1),num2str(w(feat_num+1)),'=0'];
    end
    fprintf(['决策面函数为:',express,'\n\n']);
    disp('运行LR_test开始测试');
end

LR_test.m

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
close all;
%输入测试集
test_x=rand(2,10);
%测试集样本数
test_num=size(test_x,2);
%如果误差不能满足条件，此为线性不可分问题
if i>=times
    disp('The question is not Linearly Separable');
%如果满足条件可以找到一个超平面
else
    %如果是二维特征，可以用平面坐标系绘图表示
    if feat_num==2
        hold on;
        axis([0,1,0,1])
        if w(1)==0
            line_x=[0,1];
            line_y=[-w(3)/w(2),-w(3)/w(2)];
        elseif w(2)==0
            line_x=[-w(3)/w(1),-w(3)/w(1)];
            line_y=[0,1];
        else
            line_x=[0,1];
            line_y=[-w(3)/w(2),(-w(3)-w(1))/w(2)];
        end
        %用黑色绘制分界线
        plot(line_x,line_y,'k');
        %绘制测试集样本点
        test_y=w*[test_x;ones(1,test_num)];
        for i=1:test_num
            %如果大于0，则归为一类，用红色的圈表示
            if test_y(i)>0
                plot(test_x(1,i),test_x(2,i),'ro');
            %如果小于0，则归为一类，用蓝色的圈表示
            elseif test_y(i)<0
                plot(test_x(1,i),test_x(2,i),'bo');
            %否则用绿色的圈表示
            else
                plot(test_x(1,i),test_x(2,i),'go');
            end
        end
        %说明1类对应红色，2类对应蓝色
        if (train_x(1,1)*w(1)+train_x(2,1)*w(2)+w(3)>=0&&train_y(1)==1)||(train_x(1,i)*w(1)+train_x(2,i)*w(2)+w(3)<0&&train_y(1)==0)
            %绘制训练集样本点
            for i=1:train_num
                %如果大于0，则归为一类，用红色的*表示
                if train_y(i)==1
                    plot(train_x(1,i),train_x(2,i),'r*')
                %如果小于0，则归为一类，用蓝色的*表示
                else
                    plot(train_x(1,i),train_x(2,i),'b*')
                end
            end
        %说明1类对应蓝色，2类对应红色
        else
            for i=1:train_num
                %如果大于0，则归为一类，用红色的*表示
                if train_y(i)==1
                    plot(train_x(1,i),train_x(2,i),'b*')
                %如果小于0，则归为一类，用蓝色的*表示
                else
                    plot(train_x(1,i),train_x(2,i),'r*')
                end
            end
        end
        hold off
    %如果不是两个特征不能用平面坐标系表示
    else
        disp('The Feature Is Not Two-Dimensional');
    end
end



实验结果

LR

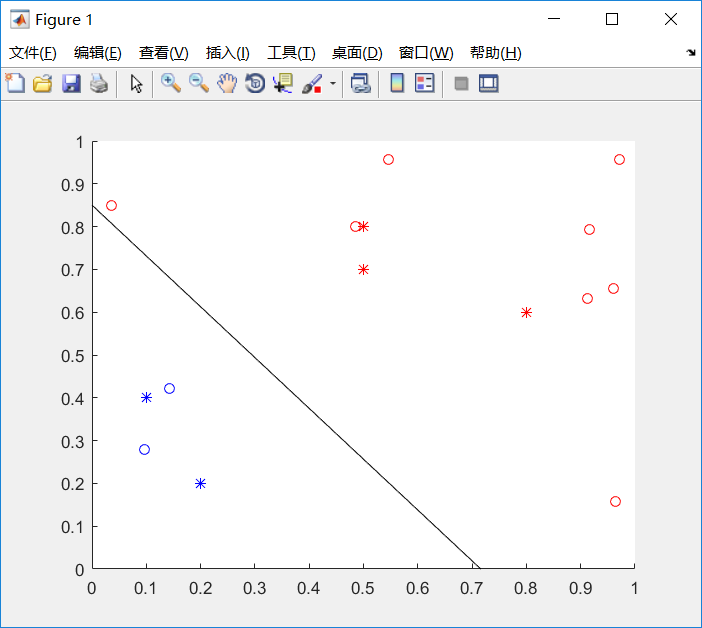
性能比较

  • 优点：
    • 算法简单，容易理解
    • 适合于大多数线性分类的任务
    • 鲁棒性较好，能够抵挡轻微噪声的影响
  • 缺点：
    • 容易欠拟合
    • 在多分类任务或者非线性任务上难以使用
    • 特征空间较大或者特征缺失情况下表现较差
-------------本文结束感谢您的阅读-------------
© 2023 USTCcoder
本站访客数 人 本站总访问量 次
0%